追加物理モジュールの紹介
ここまではAthena++を用いた磁気流体シミュレーションについて紹介してきましたが、実際の研究には問題に応じた物理過程を取り入れる必要があります。Athena++では宇宙物理学向けの多様な物理過程をサポートしていますので、ここではその幾つかを紹介します。ここで紹介しきれなかった機能や最新の追加機能については英語版のマニュアルを参照してください。
なお、残念ながらAthena++は必ずしもユーザーの方がやりたい計算がなんでも「Enterキーを押すだけでできる」というわけではありませんし、ユーザーの要望を全て開発するだけのリソースも残念ながらありません。一方で色々なことを柔軟に実装できるような設計になっていますので、思ったよりも多くのことがユーザーサイドの機能で実現できます。また、我々としては開発コミュニティも拡大したいと考えておりますので、是非ユーザー側での開発を御検討ください。「こういう機能を追加したいのだがどうしたらいいのか」という相談にはいつでも乗りますので、御気軽に御相談ください。
Athena++の最新の公開バージョンでは以下のような物理過程がサポートされています。以下について簡単な使用例を交えて紹介します。
- 拡散:粘性・熱伝導(Super Time Stepping対応)
- 非理想磁気流体効果:オーム散逸・両極性拡散(Super Time Stepping対応)
- Shearing box
- Orbital advection
- 回転系
- 自己重力(Multigrid、FFT)
- 特殊相対性理論
- メトリック固定の一般相対性理論
- 一般状態方程式(今回は省略)
なお、ここからは応用編になりますので、configureのオプションやジョブスクリプトに関して講習会環境向けのものを毎回書くことはしません。各実行環境に合わせて適宜読み替えてください。
拡散:粘性・熱伝導
1. 拡散方程式
宇宙物理学で対象とする多くの系では、分子運動論に起因する通常の意味での粘性は非常に弱く、レイノルズ数の大きな系が殆どです。しかし、原始惑星系円盤やブラックホール降着円盤などでは乱流が実効的な粘性として働き、系の進化を駆動する場合があります。本来乱流は高解像度の流体シミュレーションで直接扱うことができるものですが、それには非常に高い分解能が必要となるため、現実的な計算コストに抑えるためにこれを粘性として取り入れる(例えばα粘性と呼ばれる)モデルが使われることがあります。熱伝導についても働く現象・スケールは限定的ですが、問題によっては重要となることがあります。重要な例としては、例えば光学的に厚い極限では輻射エネルギーの輸送は拡散方程式で良く近似することができます。これらの物理過程は全て放物型(拡散型)の偏微分方程式で記述されます。最もシンプルな拡散型の方程式は次のような形をしています: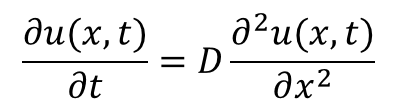
空間一次元の場合、陽解法でこれを離散化すると次のようになります: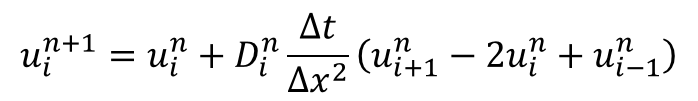
双曲型の方程式の場合と同様に、この方程式を陽的な時間積分法で安定に解くためには時間刻みに制限がかかります。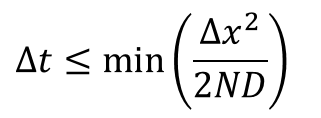
Nは空間の次元数です。ここで注目すべきは拡散型方程式の時間刻みはΔx2に比例するという点です。即ち、分解能を上げると急速に時間刻みが小さくなってしまうということを意味します(逆に、拡散は小さいスケールで強く働くと言い換えることもできます)。また、問題によっては拡散係数が大きくなるケースもあり(特に次項の非理想磁気流体効果で顕著)、メインとなる流体力学部と比べて計算コストが高くなってしまうことがあります。
このような問題に対する教科書的な対応は、時間刻みに対して制限のない陰的な解法を用いることです。上の例でいえば右辺の拡散項の評価に次の時刻n+1での値を用いることで、陰的な離散化になります。しかしこの方法は大規模な連立方程式を解くために、大域的な通信を含む複雑なプログラムが必要になり、また高次精度を実現することが困難になる、アルゴリズムによっては収束しないことがあるなど、実装するのはなかなか大変です。また、陰解法では時間刻みをCFL条件による制限を超えて大きく取ることができますが、それは安定ではあっても精度が十分かどうかとは別の問題です。もちろん問題によってはそのような陰的な解法を使用するべき場合がありますが、Athena++ではそれよりは簡単に、陽的解法を拡張したSuper time stepping(STS)という手法をサポートしています。
2. Super time stepping
CFL条件による時間刻みは「次のステップで安定である(解が非物理的な振る舞い・振動をしない)」という条件から求められたものでした。Super time stepping法ではこの制限を緩めて「Nステップ後に安定である」ことを要請します(途中のステップでの安定性は要求しません)。詳細な数学的な説明は論文を参照して頂くことにして割愛しますが、この条件の下であるルールに従って時間刻みを取ると、通常のCFL条件で決まる時間刻みを用いてNステップ進めるよりも長い時間推進が可能になります。STSについてはAlexiades et al. (1996)(オリジナル、1次精度)及びMeyer et al. (2014)(2次精度、Athena++の実装はこれに基づく)を参照してください。またSTSの適用可能範囲や極限的状況での振る舞いについてはCommerçon et al. (2011)のAppendixに例があります。
Athena++ではSTSを利用しない場合、時間刻みは最も時間スケールの短い(時間発展の速い)物理過程で決定されます。この時、全ての物理過程は同一の時間積分法(time integratorとして指定されているVL2やRK3等)で陽的に計算されます。STSを有効にすると、拡散過程(粘性・熱伝導・非理想磁気流体効果)が主の時間積分部から分離され、別のSTSを用いた時間積分部として計算されるようになります。このような手法を演算子分離法(operator splitting)と呼びます。この手法は時間スケールの大幅に異なる物理過程を導入するのに簡便な方法ですが、実装によっては時間精度が低下しますので場合によっては注意が必要です。
3. 粘性拡散の計算例
ここでは粘性による速度場の拡散のサンプルコード "src/pgen/visc.cpp"がありますので、これを使用してみましょう。拡散を有効にするには特にオプションは必要ありません。STSを使うには設定が必要ですが、まずはそのまま計算してみましょう。以下のようにコードをconfigureし、"inputs/hydro/athinput.visc"を用いて実行してみてください。"--eos isothermal"オプションは等温状態方程式を指定するオプションです。
> python configure.py --prob visc --eos isothermal(環境に合わせて読み替えてください) > make clean > make > ./athena -i athinput.visc (必要ならジョブスクリプトを作成してください)
これは一次元問題で、初期にGauss分布を持つy方向の速度が粘性で拡散していく様子のシミュレーションになっています。パラメータファイルを開いてみると、<problem>に"nu_iso = 0.25"が指定されており、これで一様な粘性係数ν=0.25を指定しています。そのまま実行すると、143タイムステップくらいかかると思います。.tabファイルが出力されますのでgnuplot等でその様子を確認してください。
次に、STSを有効にしてみましょう。これには"-sts"オプションを付けてconfigureを行います(再度make clean; makeすることをお忘れなく)。
> python configure.py --prob visc --eos isothermal -sts
次にパラメータファイルを開き、<time> "sts_integrator = rkl2"を指定してください(注:初期値に"none"が指定されていますが、そのまま実行するとエラーになります。これはあまりいい実装ではないので今後修正します)。Athena++では1次精度と2次精度のSTSをサポートしており、"rkl1"が1次精度、"rkl2"が2次精度です。1次精度の方が計算自体は高速ですが、2次精度の方が精度も高く加速できる割合も大きいので、特に理由がなければ2次精度を使うことをお薦めします。これで実行すると、時間刻みが長くなり大幅にステップ数が減っていることが確認できると思います。これは、STSなしでは拡散項によって時間刻みが制限されていたものが、STSによりその制限が緩くなったためです。計算結果をgnuplotで重ねてプロットするなどして結果を比較し、STSでもほぼ遜色ない結果が得られていることを確認してください。
更にSTSの威力を見てみましょう。上で述べた通り、流体部の時間刻みがΔt∝Δxであるのに対し、拡散部の時間刻みはΔt∝Δx2ですから、分解能を上げると両者の差はより大きくなるはずです。そこで格子点数nx1を大幅に増やして、STSの有無で計算時間を比較してみてください。
Athena++では、デフォルトでは流体部の時間刻みで計算できるようにSTSの加速パラメータを決定するようになっています。この時、解の精度・安定性が保たれているかどうかはコード側ではチェックできません。そのため、拡散部の時間刻みが非常に短い場合、解が非物理的になる程の加速が行われてしまうことがあります。実際にどの程度の加速が行われているのかは<time>に"dt_diagnostics = 0"を指定すると計算実行時に"ratio"として表示されます。問題にも依るので一概には言えませんが、2次精度のSTSで加速するのは100倍程度に留めておくのが無難です。sts_max_dt_ratioパラメータを指定することで、この加速倍率を制限することができます。
<time> sts_integrator = rkl2 sts_max_dt_ratio = 100.0 dt_diagnostics = 0
STSは「時間刻みの取り方を変えるだけで計算を加速できる」「時間刻み以外は陽解法と同じなので並列化などもそのまま利用できる」という点で実装が非常に容易で実用性の高い技術ですが、やや黒魔術的な要素を含む技術であり、利用にあたり幾つか注意が必要です。まず注意して頂きたいことは、繰り返しになりますが安定であることと精度が十分であることは別の問題であるという点です。原理的に考えれば明らかなことですが、(通常の拡散型のステンシルでは)情報はNステップで最大Nセルしか伝わりません。そのため、STSで大きな加速をして本来必要なステップ数よりも大幅に少ないステップ数で計算すると、情報の伝播速度を過小評価する傾向にあります。次に、全ての型の偏微分方程式がSTSで加速できるわけではなく、放物型(拡散型)の方程式では上手く行きますが双曲型の偏微分方程式にはほぼ無力であることが知られています。また、方程式に源泉項が付随している場合や非線形性の強い方程式系では非物理的な振る舞いをする可能性があります。STSを使う場合は必ず実計算でテストをして加速パラメータ(sts_max_dt_ratio)を適切に設定し、物理的に妥当な解が得られることを確認してから利用するようにしてください。
4. 拡散計算モジュールについての補足
上記のテストコードは2次元の設定にも対応しています。パラメータファイルで2次元の格子を設定した上で、<problem>"iprob = 1"と指定すれば、2次元空間でvzが拡散するという設定で計算を行うことができます。そのままではCFL条件が2次元の制限を超えてしまいますので、<time>"cfl_number"に0.4程度の値を指定してください。
ここでは一様・一定な粘性係数を指定した場合の拡散の計算について紹介しました。同様に一様・一定な熱伝導係数によるエネルギーの拡散も<problem>"kappa_iso"に拡散係数を指定することで実現できます。
一方、実用上は拡散係数が物理量や場所・時間の関数であるケースが多いでしょう。このような場合はユーザー指定の拡散係数を与えることができます。これには、problem generator内でphdif->nu(HydroDiffusion::DiffProcess::iso,k,j,i)及びphdif->kappa(HydroDiffusion::DiffProcess::iso,k,j,i)を計算する次のような形のユーザー定義関数を実装し、これをMesh::InitUserMeshData内でEnrollすることで実装できます。
void MyViscosity(HydroDiffusion *phdif, MeshBlock *pmb, const AthenaArray<Real> &w,
const AthenaArray<Real> &bc, int is, int ie, int js, int je, int ks, int ke) {
if (phdif->nu_iso > 0.0) {
for (int k=ks; k<=ke; ++k) {
for (int j=js; j<=je; ++j) {
#pragma omp simd
for (int i=is; i<=ie; ++i)
phdif->nu(HydroDiffusion::DiffProcess::iso,k,j,i) = ...;
}
}
}
}
void MyConduction(HydroDiffusion *phdif, MeshBlock *pmb, const AthenaArray<Real> &w,
const AthenaArray<Real> &bc, int is, int ie, int js, int je, int ks, int ke) {
if (phdif->kappa_iso > 0.0) {
for (int k=ks; k<=ke; ++k) {
for (int j=js; j<=je; ++j) {
#pragma omp simd
for (int i=is; i<=ie; ++i)
phdif->kappa(HydroDiffusion::DiffProcess::iso,k,j,i) = ...;
}
}
}
}
void Mesh::InitUserMeshData(ParameterInput *pin) {
EnrollViscosityCoefficient(MyViscosity);
EnrollConductionCoefficient(MyConduction);
}
これらのユーザー定義関数を利用する場合も、拡散モジュールを有効にするために<problem>"nu_iso"または"kappa_iso"に0より大きい値を指定する必要があります。ユーザー定義関数の実例は次の非理想磁気流体効果とほぼ同様ですので、そちらで紹介します。なお非等方な粘性・熱伝導も原理的には実装可能ですが現時点ではこれは準備段階となっており、動作しませんので御注意下さい。
拡散モジュールはSTSの有無に関わらずAMR・SMRと組み合わせて利用することができます。その他の詳細については英語版ドキュメントのDiffusion Processes及びSuper Time Steppingの項も参照してください。
非理想磁気流体効果:オーム散逸・両極性拡散
1. 非理想磁気流体効果
宇宙物理学で対象とする天体現象の多くでは、流体(ガス・プラズマ)はある程度電離されていて理想磁気流体近似(磁場とガスが凍結していて、一体となって運動する)が良く成立しています。しかし、例えば星形成過程や原始惑星系円盤等、電離度が非常に低いために磁場とガスが脱結合する領域があります。これを非理想磁気流体効果と呼び、通常の電気抵抗によるオーム散逸、正電荷と負電荷の間の分離に起因するホール効果、そして中性粒子と荷電粒子の間の分離に起因する両極性拡散の三つの効果があります。このうちオーム散逸と両極性拡散はおおよそ拡散型の振る舞いをするのに対し、ホール効果は分散型であり著しく性質が異なり、適用できる数値計算手法も異なります。ホール効果は宇宙物理学の応用上大変興味深いのですが、現時点でのAthena++の公開版ではオーム散逸と両極性拡散のみがサポートされています(ホール効果も近日公開できる予定です)ので、ここではこれらを御紹介します。
非理想磁気流体効果を含む磁場の誘導方程式は次のように書かれます: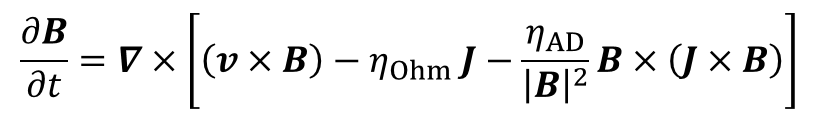
ここでJ=∇×BはMHD近似における電流密度です。また、両極性拡散は荷電粒子と中性粒子の2流体として扱うこともありますが、ここでは電離度が低いとして荷電粒子の慣性を無視し、一流体として近似しています。更にエネルギー方程式にも対応する項が現れますが、やや煩雑ですのでここでは省略します。詳しくはコード論文を参照してください。
2. 非理想磁気流体効果の計算例
非理想磁気流体効果を有効にするには、粘性・熱伝導と同様に、<problem>に"eta_ohm"または"eta_ad"を指定すれば有効になります(両方同時に指定することが可能です)。またSTSを使用することも可能です。例として、単純な磁場の拡散の例が"src/pgen/resist.cpp"(パラメータファイル"inputs/mhd/athinput.resist")にありますので、試してみてください。
更に、粘性の場合と同様に、ユーザー定義の抵抗率ηを指定することもできます。こちらについては"src/pgen/reconnection.cpp"(パラメータファイル"inputs/mhd/athinput.reconnection")に例がありますので、そちらを御覧下さい。また、高棹さんによる講義資料も御参照下さい。
Shearing box
原始惑星系円盤やブラックホール降着円盤のようなケプラー回転に近い回転プロファイルを持つ(中心重力に支配された)天体は、円盤全体をシミュレーションしようとすると内縁付近でのタイムスケールが外側と比べて非常に短いため、短い時間刻みが必要となり大きな計算資源が必要となります。これを回避するためにしばしば用いられているのがShearing boxという手法です。これは以下の図のように円盤の一部を切り出して、その近傍を局所的にシミュレーションするものです。
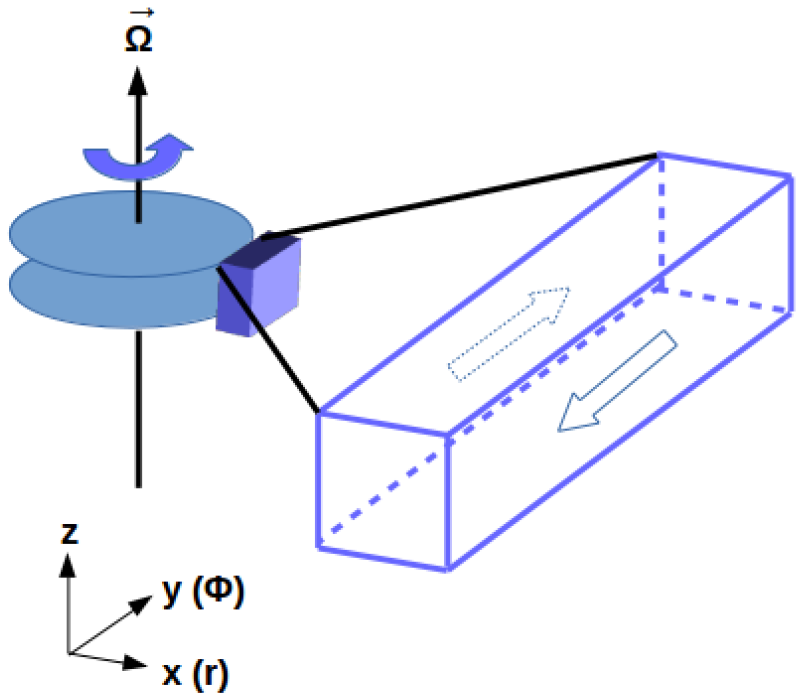
この手法は円盤の曲率や動径方向の構造など大域的な効果が取り入れられていないため適用できる問題には制限がありますが、例えば円盤内の乱流について調べたり、原始惑星系円盤中の惑星周辺の降着流の構造を調べたりと、円盤内の小スケールの構造を調べるのによく使われます。大きく分けて、鉛直(z)方向の構造がない非成層(non-stratified)と、鉛直方向の成層構造を考慮したstratifiedの二種類がありますが、Athena++コードで利用する上では特に区別はありません。Shearing boxを有効にするには、<orbital_advection>ブロックに必要なパラメータを指定します。
<orbital_advection> Omega0 = 1.0 qshear = 1.5 shboxcoord = 1
ここでOmega0は系の角速度を計算の次元に合わせて指定してください。またqshearはシアー率と呼ばれる回転プロファイルに依存する値で、ケプラー回転する円盤では1.5になります。shboxcoordはシアの方向を指定するパラメータで、2次元問題でxz平面を扱う時は2、それ以外の場合は1を指定します。これで(Omega0とqshearが共にゼロでなければ)shearing boxが有効になります。
Shearing boxでは回転方向(ここではx2)の境界条件は周期境界でなければなりません。x1方向については問題に応じて流出境界条件等を指定できますが、MRI乱流などの計算ではシア周期境界条件がよく用いられます。この場合は以下のように指定します。
<mesh> ix1_bc = shear_periodic ox1_bc = shear_periodic ... ix2_bc = periodic ox2_bc = periodic ...
Shearing boxの計算ではy方向にvy = -qΩ0xの速度場を持っていることが仮定されます。そのため初期条件・境界条件を作成するときはこれと整合的な速度場を指定してください。また、計算領域をx=0に関して対称に設定するのが自然です。また、non-stratifiedの場合は特に必要ありませんが、stratifiedの計算を行う場合には鉛直方向にしかるべき重力場と境界条件をユーザーが定義する必要があります。
シア周期境界条件を用いる計算にはtime integratorは3次精度以下でなければならない、x2方向の格子間隔が等間隔でなければならない、static mesh refinementを用いる場合はシア境界で接する可能性のあるMeshBlockは全て同じレベルでなければならない(AMRは非対応)、等の制限があります。また自己重力など一部のモジュールは互換性がありません。
Shearing boxを利用した計算例として、2次元shearing sheet("src/pgen/ssheet.cpp")、2次元MRI("src/pgen/hg3.cpp")、3次元MRI("src/pgen/hgb.cpp")のテスト問題が提供されていますので試してみてください。合わせて、公式ドキュメントのShearing Box及び小野さんの発表資料も参照して下さい。
Orbital advection
原始惑星系円盤のような低温の円盤は、音速と比べて回転速度が大きい高マッハ数の流体であり、時間刻みは主に回転速度によって決定されています。上述のShearing boxを利用している場合や、中心重力が支配的な円盤(の中心面付近)では、回転速度プロファイルが事前にわかっている場合があります。このような問題では、回転(軌道運動)を分離して解析的に計算することで、回転に起因する時間刻みを緩和することができ、特に音速が小さい系では大幅に計算を高速化できる場合があります。これを実現するのがOrbital advectionです。
Orbital advectionが使えるのは以下の場合です。
- デカルト座標でx2(y)方向の移流に対して、Shearing boxが有効またはユーザー定義の速度プロファイルが与えられている
- 円筒座標でx2(φ)方向の移流に対して、<problem>GMが指定されている(ケプラー回転)またはユーザー定義の移流速度プロファイルが与えられている
- 球座標でx3(φ)方向の移流に対して、<problem>GMが指定されている(ケプラー回転)またはユーザー定義の移流速度プロファイルが与えられている
実用上、Shearing box及び2次元円筒座標ではデフォルトの移流速度プロファイルを使うことを推奨します。一方3次元の問題では全域で移流速度を事前に決定することが困難なことが多く、必ずしもOrbital advectionが有用とは限らないことに注意してください。移流速度プロファイルの指定方法については英語版マニュアルを参照してください。利用可能な条件を満たしている時、パラメータファイルに以下のようにOAorderを指定するとOrbital advectionが有効になります。
<orbital_advection> OAorder = 2 # 0:OAなし (デフォルト)、1: OA1次精度、2: OA2次精度
OAorderはOrbital advectionの時間精度を指定するパラメータです。2次の方が高精度ですが、計算コストは少し高くなります。まずは2次精度を試してみて、計算コストが気になる場合は1次も試してみて結果があまり変わらないなら1次を使う、というのが目安になります。
Orbital advectionを使用する場合、背景速度場を差し引いた初期条件・境界条件を与える必要があります。Time integratorは3次以下、相対論は非サポートという制限がありますが、Mesh refinementとの併用も可能です。軌道運動が支配的な問題ではOrbital advectionを有効にすることで移流に起因する数値拡散を抑制することができるため、計算コストだけでなく精度の面でもOrbital advectionを使うメリットがあります。特に、Shearing boxを使用する場合はOrbital advectionを併用することをお薦めします。また、拡散系の物理で上述のSTSとOrbital Advectionを併用する場合には2次精度を指定することを推奨します。
Orbital advection使用時にはデフォルトでは静止系での速度場が出力されますが、軌道運動を差し引いた速度場が見たい場合には、outputブロックに以下のように指定することで背景速度場を差し引いた速度場を出力できます。
<output1> ... orbtal_system = true
Orbital advection(+shearing box)の使用例として3次元MRIのテスト問題("src/pgen/hgb.cpp")が提供されています。Orbital advectionを有効にして、その効果を試してみてください。また、Orbital advectionの有無による初期条件の指定の違いについてもこのコードが参考になります。
回転系
系が剛体回転に近い単純な回転則を持っている場合、問題によっては静止系で解くよりも回転系で解いた方が長い時間刻みを取れるなどのメリットがある場合があります。また、原始惑星系円盤中で惑星を固定した系で解きたい、と言う場合にも回転系は有用です。Athena++では円筒座標・球座標で<orbital_advection>ブロックにOmega0パラメータを指定することで、角速度Ω0の回転系でのシミュレーションが有効になります。
自己重力
1. ポアソン方程式の数値解法
宇宙は大域的には電気的に中性なので、大きなスケールでは重力が支配的な力となります。重力は天体を形成し、星・惑星から銀河そして宇宙全体まで全ての構造を支配する根源的な力と言っていいでしょう。宇宙物理学では中心星やブラックホールの点源重力場、あるいは銀河のポテンシャルを外場として扱うことがあり、この場合はソース関数の導入で扱ったユーザー定義のソース項として簡単に実装することができます。しかし一方で、宇宙物理学の多くの問題で流体が作り出す自己重力が重要になります。この場合、自己重力ポテンシャルφとそれによる重力場は以下のポアソン方程式で記述されます。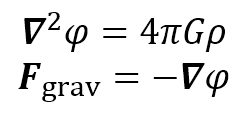
この方程式は楕円型であり、これに加えて適切な境界条件を与えることが重要になります。これを例えば3次元で2次精度で離散化すると次のようになります。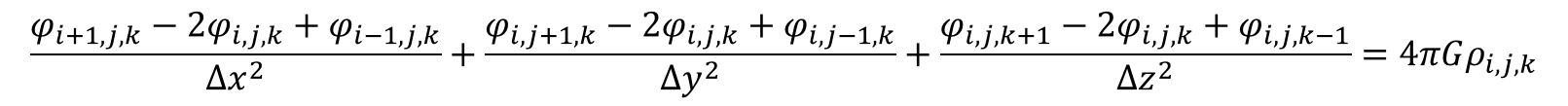
これらは流体力学方程式などよりも単純な形をしていますが、数値的には実はこちらの方が圧倒的に厄介な性質を持っています。それは、この方程式では情報の伝播速度が無限大であり、密度場の変化が即時にポテンシャルの変化として全空間に伝わるため、常に大域的な連立方程式を整合的に解く必要があるためです。空間3次元の場合N3変数の連立方程式を解くことになり、LU分解等を用いた直接法では到底計算できないコストになります。
格子法の流体コードに実装されるポアソン方程式の数値解法は大きく分けて三つあります。一つはポアソン方程式をJacobi法やGauss-Seidel法、またはCG法等の反復法を用いて解くもので、Athena++にはその発展版であるMultigrid法を用いた解法が実装されています。次の方法は、利用できる境界条件に制限がありますが、高速フーリエ変換(Fast Fourier Transform, FFT)を用いる手法で、こちらもAthena++に実装されています。最後の一つは詳しくは紹介しませんが、ガスの分布を粒子のように扱い、重力多体問題でよく使われているツリー法を用いるものです。ここではFFTとMultigridを用いた計算について主に説明します。
2. Multigrid法を用いた自己重力計算
Gauss-Seidel法のような古典的な反復法では、短波長の残差は急速に減衰させられる一方、長波長の残差を減衰させるのには多数の反復回数を要します。Multigrid法では計算の分解能を変えながらGauss-Seidel法のような反復法を適用することで、短波長の残差は高分解能の格子で、長波長の残差は低分解能の格子でそれぞれ減衰させることで、全ての波長の波を同時に減衰させることで高速に解を収束させる手法です。古典的反復法では格子点数に対して必要な反復回数が増加しますが、Multigrid法では反復回数は格子点数にほぼ依存しないため、O(N)の計算量の非常に強力なアルゴリズムであり、自己重力のポアソン方程式に対してはほぼ最適な解法の一つと考えられています。Multigridアルゴリズムの詳細については公式マニュアルのMultigridのページを参照してください。
ここではアカデミックな問題ではありますが、Jeans wave(自己重力を含む微小振幅の平面波)を例にとって解説します。対応するファイルは"src/pgen/jeans.cpp"(パラメータファイル "inputs/hydro/athinput.jeans_3d")になります。Multigridには特に外部ライブラリ等は必要ありません。configureする際のオプションに"--prob jeans"に加えて"--grav mg"を付けてください。
> python configure.py --prob jeans --grav mg(手元の計算機で実行する場合) > python configure.py --prob jeans --grav mg -mpi --mpiccmd CC(XC50で実行する場合)
この問題のパラメータファイル"athinput.jeans"の下の方には重力ソルバに関する設定が以下のように記述されています。
<gravity> mgmode = FMG threshold = 0.0 ix1_bc = periodic ox1_bc = periodic ix2_bc = periodic ox2_bc = periodic ix3_bc = periodic ox3_bc = periodic
mgmodeはMultigridソルバの動作モードの指定で、Multigrid iteration(MGI)とFull Multigrid(FMG)とのいずれかを指定します。MGIは計算開始時に初期推定値を与えてこれをMultigrid法の反復によって真の解に収束させていく古典的な方法です。一方、Full Multigridは最も粗視化した格子からスタートして、粗い格子の結果を細かい格子の初期推定値として使用する方法で、計算開始時に初期推定値を与える必要がなく、良好な収束性が得られます。実用上FMGの方が安定かつ高速なので、特段の理由がなければFMGを指定してください。thresholdは計算の収束条件を指定するパラメータで、0を指定した場合は反復によって残差が減少しなくなるまで(=できる所まで)解を収束させます。実用上そこまで解を収束させる必要は必ずしもありませんが、これが一番安全な使い方になっています。計算速度を求める場合にはthresholdの値を変えて試してみて、問題ない精度が得られる所を実験的に探す必要があります。あるいはniterationパラメータに反復回数を直接指定することも可能です。
ix?_bc, ox?_bcには境界条件を指定します。Multigrid法では周期境界条件(periodic)以外に勾配なし(zerograd)、ゼロ固定(zerofixed)、そして多重極展開を用いた孤立境界条件(multipole)が提供されており、それ以外にユーザー定義の境界条件を指定することも可能です。星形成や分子雲、銀河などの計算においては実用上multipole境界条件が重要です。この他のMultigrid法に関するパラメータについて、詳しくは公式マニュアルのSelf Gravity with Multigridを参照してください。
配布ファイルのパラメータは初期状態では<problem>"njeans = 0.5"となっており、このまま実行すると重力的に安定のため、波のまま何も起こりません。njeansは揺らぎの波長とjeans波長の比であり、njeans > 1では重力不安定になります。そこで次にこれを"njeans = 1.5"として実行してみてください。揺らぎが成長し、まずは平面波のまま高密度領域が形成された後に、幾つかの塊に分裂する様子が見られるはずです。重力ポテンシャルはphiとして出力されます。また、<gravity>にoutput_defect = trueを指定すると、Multigrid法で計算された残差(解の誤差に関係した量)を出力することもできます。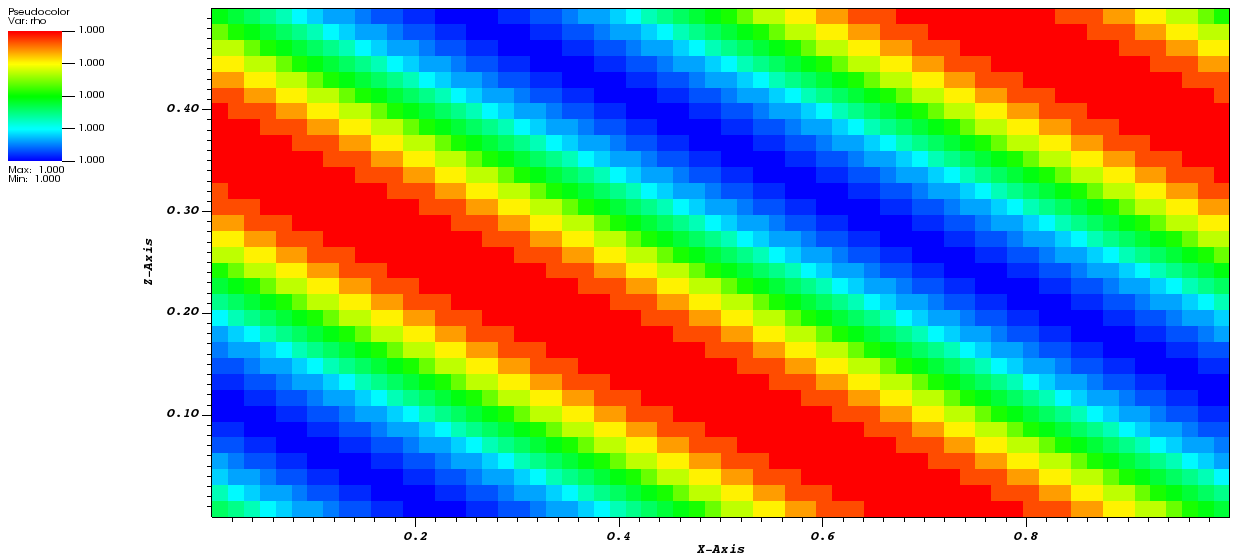
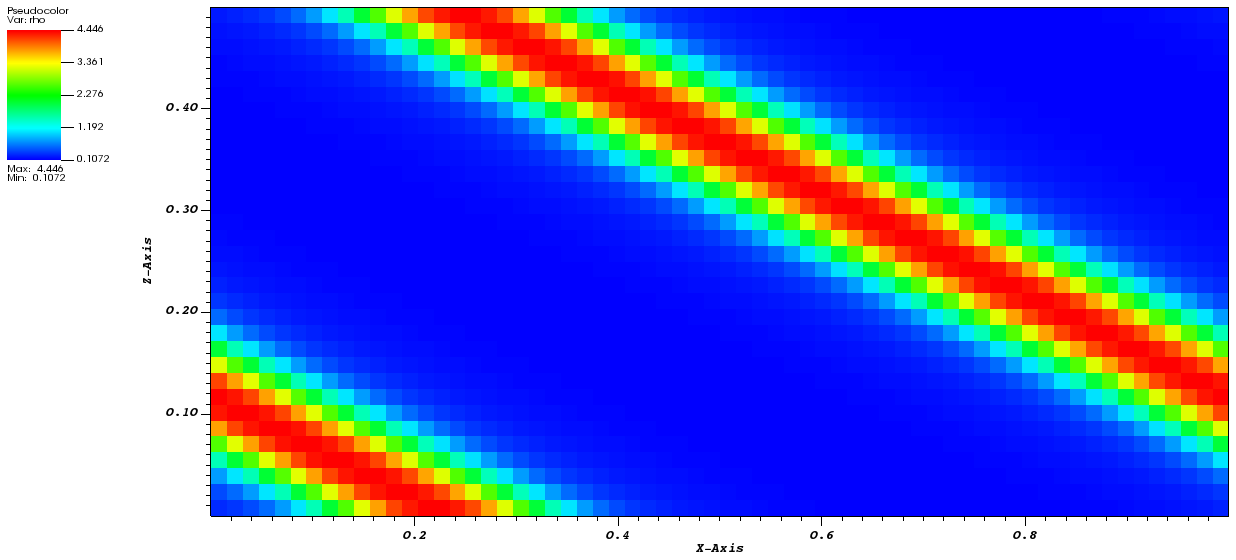
時刻t=1における密度分布。上:重力的に安定な場合、下:重力的に不安定な場合。
並列計算を行いたい場合は通常通りMeshBlockのサイズを指定すれば、同様に並列化されます。また、Multigrid法はSMR及びAMRでも利用可能です。Multigrid法では全体の格子点の数には制限はありませんが、各MeshBlockの各辺のセル数が2の冪乗の立方体でなければならないという制限があり、MeshBlockの分割を工夫する必要がある場合があります。Mesh全体として格子点数が2の冪乗の立方体になっている時に最も効率の良い計算が可能です。また、現状では格子間隔が一様な3次元デカルト座標のみのサポートとなっています。
Jeans wave以外のテスト問題としてポアソンソルバの性能を測定する"src/pgen/poisson.cpp"と、球状の分子雲のコラプスのモデル"src/pgen/collapse.cpp"が重力を含むテスト問題として提供されています。後者は実習時間内では計算が終わらないので割愛します。
Multigrid法による重力ソルバは現時点ではβテスト段階です。公開バージョンのGithubではmultigridブランチから取得することができます。御自由に利用して頂いて構いませんが、まだバグが残っている可能性もありますので、結果については御自身で責任を持って確認するようお願いします。
3. FFTを用いた自己重力計算
FFTを用いた手法では、方程式を波数空間へフーリエ変換することで、偏微分方程式を代数方程式に置き換えて解きます。sin, cos関数を基底関数として使うため、周期境界条件以外の境界条件に適用するのには工夫が必要になり、またコストも大きくなります。宇宙物理学では宇宙論的シミュレーションなど周期境界を使うケースもそれなりにありますが、より一般の問題に対してはMultigrid法の方が有利です。また、FFTによる自己重力はSMR/AMRには対応していませんので御注意下さい。
Multigridの場合と同様に、Jeans waveを例にとって解説します。まず、FFTを有効にしてコンパイルします。その前にFFTW3ライブラリ(非並列版で構いません。FFTWと互換性のあるIntel MKLも利用可能ですが、その場合はMakefileを適宜書き換えてください。)が導入されていることを確認してください。XC50では"module load fftw3"とすればOKです。configureする際のオプションには"--prob jeans"に加えて"-fft"と"--grav fft"を付けてください。
> python configure.py --prob jeans -fft --grav fft
XC50ではfftw3 moduleをloadした上で、以下のようにします。
> python configure.py --prob jeans -fft --grav fft -mpi --mpiccmd CC
Multigrid法を用いた場合と同様の結果が得られることを確認してください。また、計算サイズを変えながらMultigridとFFTで性能を比較してみてください。MultigridがO(N)の計算量なのに対し、FFTはO(NlogN)ですので、計算サイズを大きくするとMultigridが有利になります。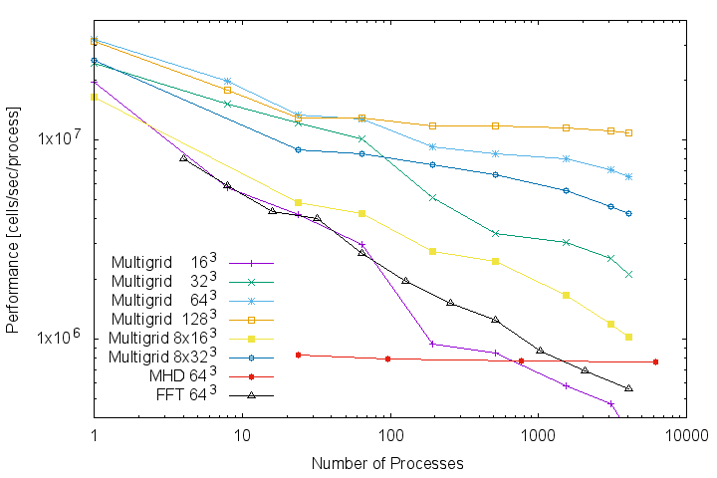
4. FFTを用いた乱流駆動・FFTによる解析
なお今回は省略しますが、Athena++ではFFTを用いて乱流を駆動するモジュールが既に実装されています。乱流駆動モジュールは初期条件にのみ乱流を導入するいわゆる"decaying"モードと、計算時間中乱流を駆動し続ける"continuous"または"impulsive"モードに対応しています。更に、パワースペクトルの解析などのためにAthena++からFFTを呼び出す仕組みも整備されています。興味のある方は"src/pgen/turb.cpp"(パラメータファイル"inputs/hydro/athinput.turb")と、英語版WikiのFFT及びTurbulence Driverを御参照下さい。
なお、FFTは任意のセル数で動作しますが、一辺のセル数が2のべき乗の時に最高の性能を発揮しますので、FFTを使用する場合にはそのような格子を使用することを推奨します。
特殊相対性理論
1. 特殊相対論的衝撃波管問題
宇宙物理学ではAGNやGRBからのジェットや超新星爆発など、多数の相対論的な現象が存在します。Athena++では特殊相対論的な流体力学・磁気流体力学をサポートしています。ここでは特殊相対論的磁気流体力学の簡単な例として(これもアカデミックな例で恐縮ですが)、1次元の衝撃波管問題を紹介します。なお初めにお断りしておきますと、これを書いている人は相対論的流体力学は専門外ですので、質問にすぐに的確に答えられない可能性もありますが御容赦ください。
相対論的な衝撃波管問題のprobem generatorは特殊相対論でも一般相対論でも"src/pgen/gr_shock_tube.cpp"を使用します。configureで"-s"オプションを指定することで特殊相対性理論が有効になります。
> python configure.py --prob gr_shock_tube -s -b
特殊相対論ではLax-Friedrichs, HLLE, HLLC, HLLD Riemann solverが利用できますが、Roe法は利用できません。また状態方程式は通常の理想的なもの(gamma-law)に限ります。座標系は非相対論の場合と同様のものが利用できます。
"inputs/hydro_sr/athinput.mb_*"(磁場なし)及び"inputs/mhd_sr/athinput.mub_*"(磁場あり)がパラメータファイルになっています。例えばmub_1を実行すると以下のような結果が得られます。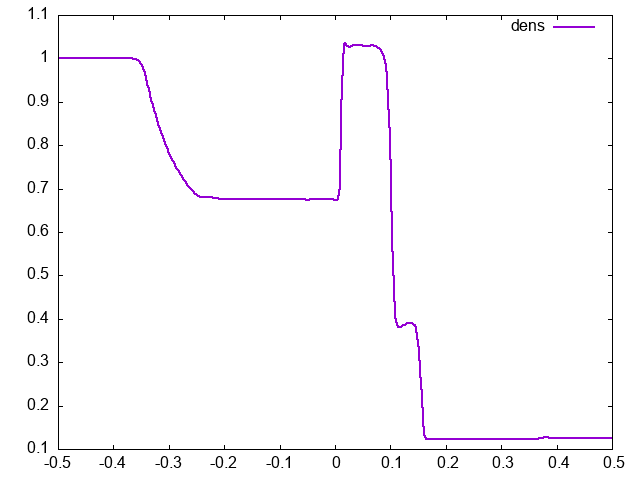
2. 特殊相対論における物理量の定義と初期条件の構築
相対論を用いて計算を行う際に留意すべき点は、初期条件の設定です。Athena++の相対論では光速度をc=1とする単位系を使用し、primitive variables(基本量)として以下の組み合わせを用います。
- 流体静止系での質量密度 ρ
- 四元速度ベクトルの空間成分 u i
- ガス圧力 pgas
- (MHDでは更に磁場B i)
またconservative variables(保存量)は以下の組み合わせになります。
- 計算の座標系での質量密度D = γρ
- 全エネルギー密度E = γ 2wtot − ptot − b tb t
- 運動量密度の空間成分M i = γ 2wtot v i − b tb i
ただし、各記号は以下のように定義されます。
- ローレンツ因子γ = (1 + u1u1 + u2u2 + u3u3)1/2
- 3次元速度 v i = u i/γ
- 四元ベクトル磁場の射影成分 b t = γ v⋅B と b i = B i/γ + b tv i
- 磁気圧 pmag = ημνb μb ν/2
- 全圧力ptot = pgas + pmag
- 断熱指数 Γ
- 流体静止系でのガスのエンタルピーwgas = ρ + Γ/(Γ−1) × pgas
- 流体静止系での磁場のエンタルピーwmag = 2pmag,
- 流体静止系での全エンタルピー wtot = wgas + wmag
非相対論の場合と同様にProblemGenerator内では保存量を指定する必要がありますが、相対論ではこれらの変換はやや面倒です。そこで、peos->PrimitiveToConserved関数を用いて変換するのが便利です(この関数は非相対論でも使えます。一般の状態方程式を使用している際に初期条件の計算をするのにもこれを使うのが便利です)。衝撃波管問題のProblemGeneratorの一部を簡略化したものは以下のようになります。
for (int k=ks; k<=ke; ++k) {
for (int j=js; j<=je; ++j) {
for (int i=is; i<=ie; ++i) {
if (pcoord->x1v(i) < 0.0) {
rho = rho_left;
pgas = pgas_left;
vx = vx_left;
vy = vy_left;
vz = vz_left;
bbx = bbx_left;
bby = bby_left;
bbz = bbz_left;
} else {
Real rho = rho_right;
Real pgas = pgas_right;
Real vx = vx_right;
Real vy = vy_right;
Real vz = vz_right;
Real bbx = bbx_right;
Real bby = bby_right;
Real bbz = bbz_right;
}
// Construct 4-vectors
Real u0 = std::sqrt(1.0 / (1.0 - (SQR(vx)+SQR(vy)+SQR(vz))));
Real u1 = ut * vx;
Real u2 = ut * vy;
Real u3 = ut * vz;
Real b0 = bbx*ux + bby*uy + bbz*uz;
Real b1 = (bbx + bt * ux) / ut;
Real b2 = (bby + bt * uy) / ut;
Real b3 = (bbz + bt * uz) / ut;
// Set hydro primitives
phydro->w(IDN,k,j,i) = rho;
phydro->w(IPR,k,j,i) = pgas;
phydro->w(IVX,k,j,i) = u1;
phydro->w(IVY,k,j,i) = u2;
phydro->w(IVZ,k,j,i) = u3;
// Set cell-centered magnetic fields
bb(IB1,k,j,i) = b1 * u0 - b0 * u1;
bb(IB2,k,j,i) = b2 * u0 - b0 * u2;
bb(IB3,k,j,i) = b3 * u0 - b0 * u3;
}
}
}
peos->PrimitiveToConserved(phydro->w, bb, phydro->u, pcoord, is, ie, js, je, ks, ke);
詳細については英語版WikiのSpecial RelativtyやRelativtyのチュートリアルのページ及び"src/pgen/gr_shock_tube.cpp"も参照してください。
一般相対性理論
一般相対論的磁気流体の計算例
Event Horizon Telescopeによる観測で話題になったM87のように、ブラックホールの強重力場周辺の構造をシミュレーションするには一般相対性理論が必要です。公開版のAthena++ではメトリック(座標系)が時間的に一定な場合の一般相対性理論がサポートされています。(時間発展するメトリックを流体と整合的に解く、いわゆるFull GRのコード GRAthena++も開発されましたが、こちらはまだ非公開です。)
ここでは特殊相対論の時よりは本格的に、 Fishbone & Moncrief (1976)の回転するブラックホール周囲のトーラス(にポロイダル磁場を入れたもの)を例に計算してみます。これは古典的な論文ではありますが、現在でもブラックホール周囲の降着流の初期条件としてしばしば使われる設定です。これに対応するProblem Generatorは"src/pgen/gr_torus.cpp"です。一般相対論を有効にするには"-g"オプションを付け、更に座標系を指定する"--coord"オプションを指定します。座標系には"minkowski", "schwarzschild", "kerr-schild"が指定できますが、ここでは回転するブラックホール周りの時空に対応する"kerr-schild"を指定します。これは多少計算コストのかかる例なのと、static mesh refinementを使用しますので、以下の例ではMPIとHDF5を有効にし、XC50を使用することを想定して"--mpiccmd CC"を指定しています。更に、PPMを使用しますので"--nghost=4"オプションもつけています。
> python configure.py -b -g --coord kerr-schild --flux hlle --prob gr_torus -mpi -hdf5 --nghost=4 --mpiccmd CC
なお、上の例では安定性と計算コスト節約のためにHLLEソルバを指定しました。Athena++では特殊相対論対応のRiemann Solverは全て一般相対論でも使用することができます(ただし、一般相対論ではHLLDは不安定になりやすいので、開発者曰くHLLEを使うのがお薦めとのことです)。HLLC(流体)またはHLLD(磁気流体)を使用する場合には、局所的なMinkowski座標系に変換して計算するための"-t"オプションを同時に指定する必要があります。HLLE及びLax-Friedrichsソルバではこれは指定してもしなくても動作します。また、状態方程式に関しても、特殊相対論の場合と同様に理想的な状態方程式(gamma-law)のみのサポートとなっています。
計算を実行するには"inputs/mhd_gr/athinput.fm_torus"ファイルを使用します。この例ではstatic mesh refinementを利用して、トーラスを高解像度で分解するよう格子を生成します。この例ではMeshBlockが72個生成されます(SMRのチュートリアルでやったように"mesh_structure.dat"を確認してください)ので、72並列で計算しましょう。ジョブスクリプトの例は以下のようになります。
#PBS -q [queue]
#PBS -l nodes=2
#PBS -l walltime=4:00:00
#PBS -N fm_torus
cd ${PBS_O_WORKDIR}
aprun -n 72 -N 36 -S 18 ./athena -i athinput.fm_torus -t 3:50 > log
72並列でもそれなりに時間のかかる計算なので待ちましょう(講習会時間中には終わらないと思います)。解像度が落ちることを承知でSMRなしで計算しても構いませんし、もう少しMeshBlockを細かくして並列数を増やして計算しても構いません。
計算が終わったらVisItで可視化してみましょう。Kerr-schild座標は論理的には球座標に近いので、極座標のチュートリアルでやった例のように、球座標からデカルト座標に変換して表示します。このトーラスは磁場がなければ平衡解になっていますが、磁場によって角運動量が輸送されることで、トーラスがブラックホールへとゆっくりと落下する様子が見られると思います。この設定では大体t=50程度まで計算すれば、降着流の構造が進化する様子が見られるはずです。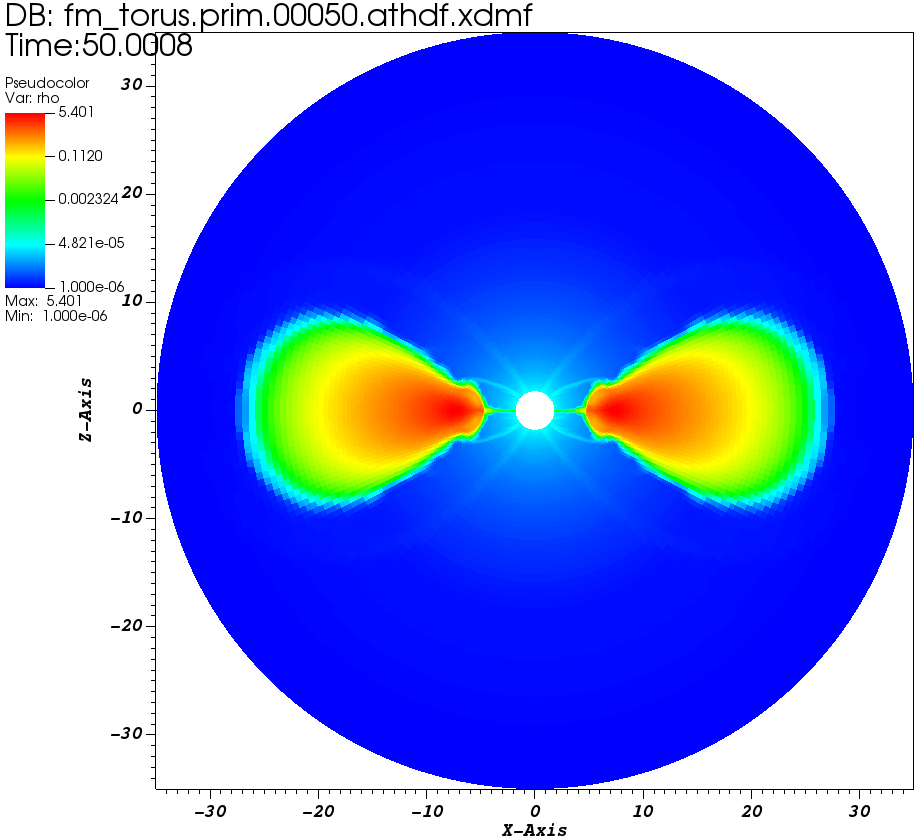
パラメータファイルの<coord>ブロックで座標系のパラメータを指定することができます。特に重要なパラメータはブラックホールの質量mとスピンパラメータa(a=0は無回転、a=1が最大回転)です。
<coord> m = 1.0 # black hole mass M a = 0.5 # black hole spin a (0 <= a/M < 1) h = 1.0 # grid compression parameter
またそれ以外にも<problem>ブロックで多数のトーラスに関するパラメータを指定することができます。興味があれば各自試してみてください。
一般相対論での初期条件の構築は複雑で本講習会の範囲を大きく超えてしまいますので割愛します。興味がある方は英語版WikiのGeneral RelativityやRelativityのチュートリアル、各種Problem Generatorなどを参考にしてください。