The Sérsic Constant

The Sérsic Profile is introduced here. So I won't go to the details. It is used to fit the light distribution from the galaxies, it's most simplest form is:

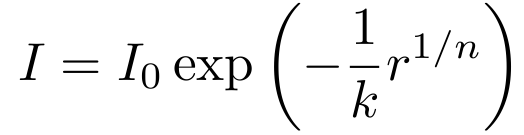
But this form does not explicitly give any information about the size of the galaxy. The width of this profile can be set through k; the lower the value of k, the wider the profile. But astronomers usually write it in this form:

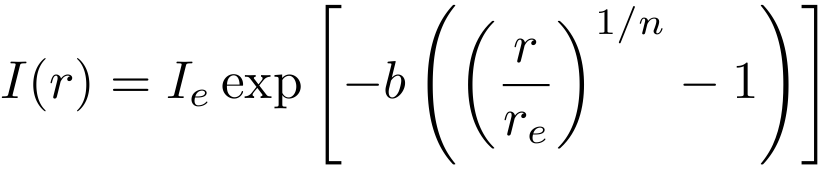
The benifit with this form of writing the Sérsic profile is that it splits the old k to b and r_e. This form enables us to define the effective radius, which is a measure of the width of the profile and is defined as: the radius containing half of the total profile light, or:

The 2πr was multiplied because we have to integrate over a surface. So, to satisfy the definition or r_e, we have to set b to a particular value to satisfy this condition. Having chosen I_e (The intensity at the effective radius) and r_e, we see that the only parameter that b depends on is n.

A really good approximation for b(n) can be found in MacArthur, Courteau & Holtzman 2003; they find this very good approximation:

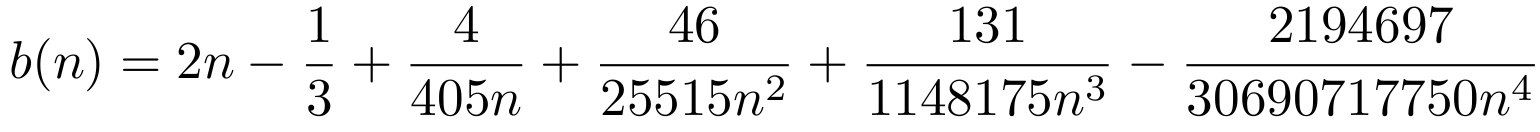
But this is only good for n>0.35, for values of n smaller than 0.35 this will not work. So you have to solve the above integrals numerically to fit your need. For my research, I had to write such a program and I made a table with one column being n values and one column being the appropriate b(n) values. The b(n) values are accurate to 0.00001 and I have done the calculation for 0.049<n<0.360, with steps of 0.001, I am leaving the results here in the hope that it can be useful for others too.

Table of b values

Python 3 program to generate the table

LaTeX codes to generate the integrals in this page.

 

This page was created on April 27th, 2012.